Question

What are the discontinuity and zero of the function f(x) = quantity x squared plus 5 x plus 6 end quantity over quantity x plus 2?

A. Discontinuity at (−2, 1), zero at (3, 0)

B. Discontinuity at (−2, 1), zero at (−3, 0)

C. Discontinuity at (2, 5), zero at (3, 0)

D. Discontinuity at (2, 5), zero at (−3, 0)

Answer 1

B. Discontinuity at (−2, 1), zero at (−3, 0)

Explanation:

The given function is:

`(x^(2)+5x+6)/(x+2)`

The expression in numerator can be expressed as factors as shown below:

`(x^(2)+5x+6)/(x+2)\\\\ =(x^(2)+2x+3x+6)/(x+2)\\\\ =(x(x+2)+3(x+2))/(x+2)\\\\ =((x+2)(x+3))/(x+2)`

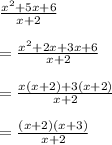
Note that for x = -2, both numerator and denominator will be zero. When both the numerator and denominator of a rational function are zero for a given value of x we get a discontinuity at that point. This discontinuity is known as a hole. This means there is a hole at x = -2

Cancelling the common factor from numerator and denominator we get the expression f(x) = x + 3

Using the value of x = -2 in previous expression we get:

f(x) = -2 + 3 = 1

Thus, there is a discontinuity(hole) at (-2, 1)

For x = -3, the value of the expression is equal to zero. This means x = -3 is a zero or root of the function.

Thus, (-3, 0) is a zero of the function.

Therefore, option B would be the correct answer.