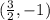Question

Solve the following system of equations
2x – 3y = 6
4x+2y=4​

Answer 1

`\boxed{((3)/(2) ,-1)}`

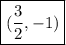
Explanation:

`\left \{ {{2x-3y=6} \atop {4x+2y=4}} \right.`

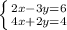
It seems this system of equations would be solved easier using the elimination method (the x and y values are lined up).

Multiply everything in the first equation by -2 (we want the 4x to be able to cancel out with a -4x).

`2x-3y=6 \rightarrow -4x+6y=-12`

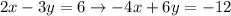
Now line up the equations (they are already lined up - convenient) and add them from top to bottom.

`\left \{ {{-4x+6y=-12} \atop {4x+2y=4}} \right.`

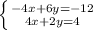
The -4x and 4x are opposites, so they cancel out.

Adding 6y and 2y gives you 8y, and adding -12 and 4 gives you -8.

`8y=-8`

Divide both sides by 8.

`y=-1`

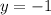
Since you have the y-value you can substitute this in to the second (or first equation, it doesn't necessarily matter) equation.

`4x +2(-1)=4`

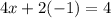
Simplify.

`4x -2=4`

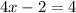
Add 2 to both sides.

`4x=6`

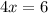
Divide both sides by 4.

`x=(6)/(4) \rightarrow(3)/(2)`

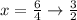
The final answer is
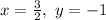`x=(3)/(2) ,~y=-1`.

`((3)/(2) ,-1)`