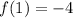Answer:
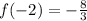
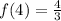
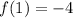
Explanation:
For this case it has a piecewise function composed of two functions.
To evaluate the piecewise function observe the condition.
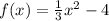 when
when
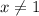
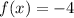 when
when
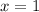
We start by evaluating
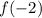 , note that
, note that
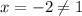 . Then we use the quadratic function:
. Then we use the quadratic function:
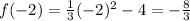
Now we evaluate
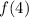 note that
note that
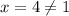 . Then we use the quadratic function:
. Then we use the quadratic function:
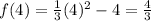
Finally we evaluate
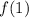 As
As
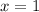 then
then