Question

Solve the system of linear operations

Answer 1

`\boxed{(-2,1)}`

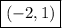
Explanation:

`\left \{ {{5x+2y=-8} \atop {x+4y=2}} \right.`

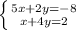
I'll be solving this system of equations using the elimination method since the x and y values are neatly lined up.

I want to get a pair of x's or y's that cancel out, and it looks like the easiest way to start would be by multiplying the first equation by -2 (the y's will cancel).

I chose to multiply the first equation by -2 instead of multiplying the second equation by 5 because -2 is a smaller number and easier to multiply by.

`-2*(5x+2y=-8)`

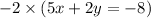
Distribute -2 inside the parentheses. Now you've got:

`\left \{ {{-10x-4y=16} \atop {x+4y=2}} \right.`

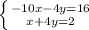
Add up the equations from top to bottom.

-10x plus x is -9x, the -4y and 4y cancel out, and 16 plus 2 is 18. Make this one single equation.

`-9x=18`

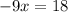
Divide both sides by -9.

`x=-2`

Substitute this value of x into the second equation (less to do with the x since it has no coefficient which means no multiplying).

`(-2)+4y=2`

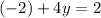
Add 2 to both sides.

`4y=4`

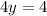
Divide both sides by 4.

`y=1`

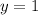
The final answer is
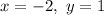`x=-2, ~y=1`.