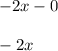Question

Given the function g(x)= 5-x^2, simplify the bottom

Answer 1

`-2x`

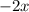
Explanation:

We are given the function
`g(x)=5-x^2` and the expression
`\lim_(x \to 0)  (g(x+h)-g(x))/(h)`

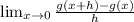
First, we must substitute in x+h into g(x) and substitute in g(x) into the expression

`\lim_(h \to 0)(5-(x+h)^2-(5-x^2))/(h) \\`

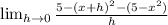
Next, we can simplify by multiplying out the exponents and then combine like terms

`\lim_(h \to 0)(5-(x+h)^2-(5-x^2))/(h) \\\\\lim_(h \to 0)(5-x^2-2xh-h^2-5+x^2)/(h) \\\\\lim_(h \to 0)(-2xh-h^2)/(h) \\`

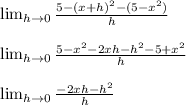
Next, we can divide the numerator by the denominator to get

`\lim_(h \to 0)(-2xh-h^2)/(h)\\\\\lim_(h \to 0) -2x-h`

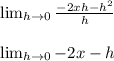
Lastly, we can substitute in 0 for h

`-2x-0\\\\-2x`