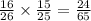Question

A hat contains slips of paper with the names of the 26 other students in Eduardo's class on them, 10 of whom are boys. To determine his partners for the group project, Eduardo has to pull two names out of the hat without replacing them.

What is the probability that both of Eduardo's partners for the group project will be girls?

Answer 1

`(24)/(65)`

Explanation:

Total number of students in the class = 26

Number of boys in the class = 10

Number of girls in the class = 26 - 10 = 16

The formula for probability is :

`\text{Probability}=\frac{\text{Favorable Outcomes}}{\text{Total Outcomes}}`

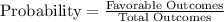
In this case the favorable outcomes would be the number of girls in the class and total outcomes would be the total number of students in the class.

Eduardo has to pull out two names from the hat. Since there are 16 girls in the class of 26, the probability that the first name will be of the girl will be =
`(16)/(26)`

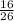
After picking up the 1st name, there would be 25 names in the hat with 15 names of girls as one of the girl is already been chosen. So,

The probability that the second name would belong to a girl =
`(15)/(25)`

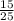
The probability that both the partners will be girls will be equal to the product of two individual probabilities as both the events are independent.

Therefore,

The probability that both of Eduardo's partners for the group project will be girls =
`(16)/(26) * (15)/(25) = (24)/(65)`