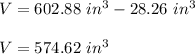Question

4.

A 48 inch long cylindrical shaped cannon has a diameter of 4 inches. There are two 3 inch diameter cannonballs inside it. How much empty space is in the cannon barrel (round to the nearest hundredth and use 3.14 for pi)?

Answer 1

`574.62\ in^3`

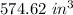
Explanation:

First we calculate the volume of the cylinder.

`V=\pi r^2*l`

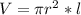
Where r is the radius and l is the length of the cylinder.

We know that:

`r = (diameter)/(2)`

`r = (4)/(2)`

`r = 2\ in`

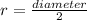
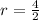
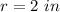
Then:

`V=3.14* 2^2*48`

`V=602.88\ in^3`

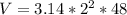
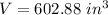
Assuming that the cannon balls are spherical then the volume of the 2 spheres is:

`V=2*(4)/(3)\pi r^3`

`V=2*(4)/(3)(3.14)((3)/(2))^3`

`V=2*(4)/(3)(3.14)((3)/(2))^3`

`V=28.26\ in^3`

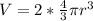
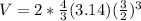
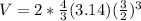
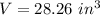
So the space left inside the cannon is

`V=602.88\ in^3 - 28.26\ in^3\\\\V=574.62\ in^3`