Question

Solve (x + 2<5) n (x-7>-6).
{x11 {x1x < 3 or x> 1)
{all real numbers)

Answer 1

For this case we must solve
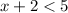`x + 2 <5`intersected with
`x-7> -6`

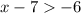
So, we have:

`x + 2 <5\\x <5-2\\x <3`

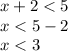
The solutions are given by all strict minor numbers to 3.

`x-7> -6\\x> -6 + 7\\x> 1`

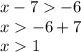
The solutions are given by all the major strict numbers to 1.

If we intersect the solutions of both equations we have
`x <3` ∩
`x> 1`.

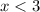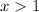The intersection is given by
`1 <x <3`

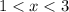
Answer:

The solution interval is (1,3)