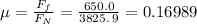Answer:
The coefficient of kinetic friction
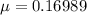
Step-by-step explanation:
From Newton's second law
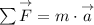
If the velocity is constant, that means the summation of all forces must be equal to zero. Draw the free-body diagram to obtain the sums of forces in x and y. It must include the Friction Force, in the opposite direction of the displacement, the weight (
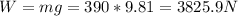 ), the Normal Force, which is the is the consequence of Newton's third law and the forces from the two workers.
), the Normal Force, which is the is the consequence of Newton's third law and the forces from the two workers.
The sum in y is:
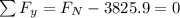
Solving for the
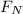 :
:
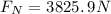
The sum in x is:
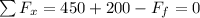
Solving for the
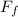 :
:
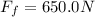
The formula of the magnitude of the Friction force is
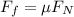
That means the coefficient of friction is: