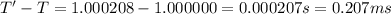Question

A pendulum clock with a brass suspension system is calibrated so that its period is 1 s at 20 degree C. If the temperature increases to 43 degree C, by how much does the period change? Answer in units of s.

Answer 1

0.207 ms

Step-by-step explanation:

First of all we need to find the length of the pendulum at 20 degrees. We know that the period is 1 s, and the formula for the period is

`T=2\pi \sqrt{(L)/(g)}`

where L is the length of the pendulum and g is the gravitational acceleration. Solving the equation for L and using T = 1 s and g = 9.8 m/s^2, we find

`L=g((T)/(2\pi))^2=(9.8) ((1)/(2\pi))^2=0.248237 m`

Now we can find the new length of the pendulum at 43 degrees; the coefficient of thermal expansion of brass is

`\alpha =18\cdot 10^(-6) 1/^(\circ)C`

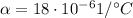
And the new length of the pendulum is given by

`L' = L (1+\alpha \Delta T)`

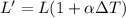
where in this case

`\Delta T = 43-20 = 23^(\circ)` is the change in temperature

Substituting,

`L'=(0.248237)(1+(18\cdot 10^(-6))(23))=0.248340 m`

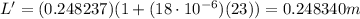
So we can now calculate the new period of the pendulum:

`T'=2\pi \sqrt{(L')/(g)}=2\pi \sqrt{(0.248340)/(9.8)}=1.000208 s`

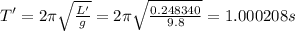
So the change in the period is

`T'-T=1.000208 - 1.000000 = 0.000207 s = 0.207 ms`