Answer:
6pm
Explanation:
Assumption: Both Dan and Phil both depart from the same station and arrive at the same station. (i.e they both travel the same distance)
Dan's travel speed is 75mph and Phil's travel speed is 60mph
Let Dan's travel time be
 and Phil's travel time be
and Phil's travel time be
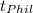
Use Formula Distance travelled = speed x time, hence
Dan's Distance Travelled =75

Phil's Distance Travelled =60
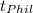
Because they travel the same distance, we can equate the 2
75
 = 60
= 60
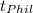
or
 = (60/75)
= (60/75)
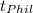
 = 0.8
= 0.8
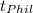 -------> eq 1
-------> eq 1
We also know that Dan left at 10:00 and Phil left at 8:00. If they end up being at the same place, this means that Phil's journey will be 2 hours longer than Dan, or
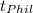 =
=
 + 2------> eq2
+ 2------> eq2
we can solve the system of 2 equations to get
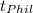 = 10 hrs
= 10 hrs
 = 8 hrs
= 8 hrs
If Phil left at 8:00 am, he will be in the same place as Dan at 8:00 + 10 hrs = 6 pm.
Double Check:
If Dan left at 10:00, he will be in the same place as Phill at 10:00 + 8 hrs = 6 pm.