Question

All objects moving in a circle experience a centripetal force. The form of centripetal force depends on the object in circular motion and the force causing the circular movement. Which of the following describes the correct centripetal force acting on an object moving in a circle?

The force of air resistance as a car drives around a corner.
The force of gravity as a satellite orbits a planet.
The force of air resistance as a ball on a string is spun in a circle.
The force of inertia as a person spins on a ride at an amusement park.

What is the maximum speed at which a car can safely travel around a circular track of radius 55.0 m if the coefficient of friction between the tire and road is 0.350?

2.60 m/s
4.39 m/s
13.7 m/s
43.0 m/s

Ciara is swinging a 0.015 kg ball tied to a string around her head in a flat, horizontal circle. The radius of the circle is 0.70 m. It takes the ball 0.60 seconds to complete one full circle. Calculate the tension in the string and its direction that provides the centripetal force acting on the ball to keep it in the circular path.

0.0077 N, toward the center of the circle
1.2 N, toward the center of the circle
0.0077 N, along the line tangent to the circle
1.2 N, along the line tangent to the circle

Answer 1

1. The force of gravity as a satellite orbits a planet.

2. 13.7 m/s

3. 1.2 N, toward the center of the circle

Step-by-step explanation:

I took the exam

Answer 2

1. The force of gravity as a satellite orbits a planet.

According to Newton's first law, an object stays at rest (or continue its motion with constant velocity) if the net force acting on it is zero.

This means that in order to have a circular motion (where the velocity changes, because the direction of motion constantly changes), we must have a net force acting on the object. This force is called centripetal force, and it always acts towards the centre of the circular trajectory.

An example of circular motion is a satellite orbiting a planet - in this case, the force of gravitational attraction between the planet and the satellite acts as centripetal force, keeping the satellite in circular motion.

2. 13.7 m/s

The centripetal force acting on an object is given by:

`F=m(v^2)/(r)`

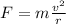
where

v is the speed of the object

m is its mass

r is the radius of the trajectory

In this situation, the centripetal force is provided by the frictional force, which is given by

`F_f = \mu mg`

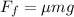
where

`\mu` is the coefficient of friction between the tire and the road

g = 9.8 m/s^2 is the acceleration due to gravity

Equalizing the two forces,

`(v^2)/(r)=\mu g`

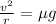
where we have:

r = 55.0 m is the radius of the track

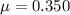`\mu=0.350` is the coefficient of friction

Solving for v, we find the maximum speed that the car can substain:

`v=√(\mu g r)=√((0.350)(9.8)(55.0))=13.7 m/s`

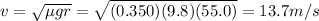
3. 1.2 N, toward the center of the circle

In this situation, the tension in the string provides the centripetal force that keeps the ball in circular motion, so we can write:

`T=m(v^2)/(r)`

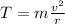
where

T is the tension in the string

m = 0.015 kg is the mass of the ball

r = 0.70 m is the radius of the circle

v is the speed of the ball

Since the ball takes t = 0.60 s to complete one full circle, its speed is

`v=(2\pi r)/(t)=(2\pi (0.70))/(0.60)=7.33 m/s`

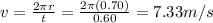
So now we can calculate the tension in the string:

`T=m(v^2)/(r)=(0.015)((7.33)^2)/(0.70)=1.15 N\sim 1.2 N`

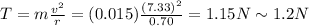
And we said previously, since this force acts as centripetal force, its direction is towards the centre of the circle.