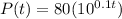Answer:
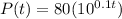
Explanation:
The 'y' axis represent log(P), so it may be modeled as a line (or linear function), where its slope is 0.1:
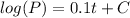
Pow each part of the equation by 10:
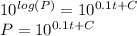
Evaluate at t=0, where the population is known.

Applying logarithmic properties:
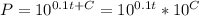
So, the final function is: