Question

Consider the following system of equations. -10x2-10y2=-300 5x2+5y2=150 Which statement describes why the system has infinite solutions?

Which statement describes why the system has infinite solutions?
The equations represent parabolas that result in graphs that do not intersect.
The equations represent circles that result in graphs that do not intersect.
The equations represent parabolas that result in the same graph.
The equations represent circles that result in the same graph.

Answer 1

The equations represent circles that result in the same graph.

Explanation:

we have

`-10x^(2)-10y^(2)=-300`

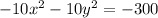
Divide by -10 both sides

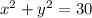`x^(2)+y^(2)=30` -----> equation A

This is the equation of a circle centered at origin with radius
`r=√(30) \ units`

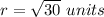
and

`5x^(2)+5y^(2)=150`

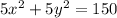
Divide by 5 both sides

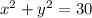`x^(2)+y^(2)=30` -----> equation B

This is the equation of a circle centered at origin with radius
`r=√(30) \ units`

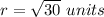
equation A and equation B are equal

therefore

The system has infinite solutions, because the equations represent circles that result in the same graph.