Question

Please assist me with these problems.
​

Answer 1

c for the question that says what point is on
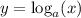`y=\log_a(x)` given the options.

9 for the question that reads: "If
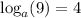`\log_a(9)=4`, what is the value of
`a^4`.

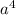Explanation:

We are given
`y=\log_a(x)`.

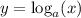There are some domain restrictions:

`a \text {is number between } 0 \text{ and } 1 \text{ or greater than } 1`

`x \ge 0`

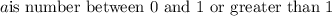
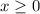
a) couldn't be it because x=0 in the ordered pair.

b) isn't is either for the same reason.

c) \log_a(1)=0 \text{ because } a^0=1[/tex]

So c is so far it! Since (x,y)=(1,0) gives us
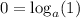`0=\log_a(1)` where the equivalent exponential form is as I mentioned it two lines ago.

d) Let's plug in the point and see: (x,y)=(a,0) implies
`0=\log_a(a)`.

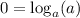The equivalent exponetial form is
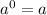`a^0=a` which is not true because
`a^0=1 (\\eq a)`.

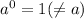If
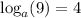`\log_a(9)=4`. then it's equivalent exponential form is:
`a^4=9`.

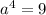Guess what it asked for the value of
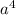`a^4` and we already found that by writing your equation
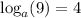`\log_a(9)=4` in exponential form.

Note:

The equivalent exponential form of
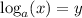`\log_a(x)=y` implies
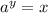`a^y=x`.