Question

3. Joe Henry’s machine shop uses 10,000 brackets during the course of a year. These brackets are purchased from a supplier 90 miles away. The following information is known about the brackets: (12 points) Annual demand 12,000 Holding cost per bracket per year $2.50 Order cost per order $60.00 Lead time 10 days Working days per year 250 a. Given the above information, what would be the economic order quantity (EOQ)? b. Given the EOQ, what would be the average inventory? What would be the annual inventory holding cost? c. Given the EOQ, how many orders would be made each year? What would be the annual order cost? d. Given the EOQ, what is the total annual cost of managing the inventory? e. What is the time between orders? f. What is the reorder point (ROP)?

Answer 1

a. 759 units

b. $948.75

c. 16 orders, $960

d. $1908.75

e. 16

f. 480

Step-by-step explanation:

Economic order quantity (EOQ) is focus on the reducing the cost like - carrying cost, holding cost to produce additional number of a units in a company.

a. The economic order quantity (EOQ) is computed below.

=
`\sqrt{\frac{2* \text{annual demand}* \text{ordering cost}}{\text{carrying cost per order}}}`

=
`\sqrt{\frac{2* \text{12,000}* \text{\$ 60}}{\text{2.50}}}`

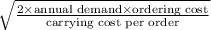
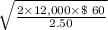
= 759 units

b. Average inventory = Economic order quantity ÷ 2

= 759 ÷ 2

= 379.5

Annual inventory holding cost = Average inventory × holding cost per order

= 379.5 × $2.50

= $948.75

c. Number of orders each year = Demand ÷ Economic order quantity

= 12,000 ÷ 759 units

= 16 orders

Annual order cost = Number of orders × ordering cost

= 16 orders × $60.00

= $960

d. Annual cost = Annual inventory holding cost + Annual order cost

= $948.75 + $960

= $1908.75

e. Time between orders = Number of working days per year ÷ number of orders

= 250 ÷ 16

= 16

f. Reorder Point (ROP) = Daily demand × lead time + safety stock

= (12,000 ÷ 250) × 10

= 480

Thus,

a. 759 units

b. $948.75

c. 16 orders, $960

d. $1908.75

e. 16

f. 480