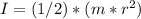Question

An old millstone, used for grinding grain in a gristmill, is a solid cylindrical wheel that can rotate about its central axle with negligible friction. The radius of the wheel is 0.330 m. A constant tangential force of 200 N applied to its edge causes the wheel to have an angular acceleration of 0.936 rad/s2. (a) What is the moment of inertia of the wheel (in kg · m2)?

Answer 1

The answer is I=70,513kgm^2

Step-by-step explanation:

Here we will use the rotational mechanics equation T=Ia, where T is the Torque, I is the Moment of Inertia and a is the angular acceleration.

When we speak about Torque it´s basically a Tangencial Force applied over a cylindrical or circular edge. It causes a rotation. In this case, we will have that T=Ft*r, where Ft is the Tangencial Forge and r is the radius

Now we will find the Moment of Inertia this way:

`Ft*r=I*a` ->
`(Ft*r)/(a) = I`

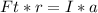Replacing we get that I is:

`I=(200N*0,33m)/(0,936rad/s^2)`

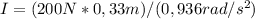
Then
`I=70,513kgm^2`

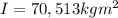
In case you need to find extra information, keep in mind the Moment of Inertia for a solid cylindrical wheel is:

`I=(1/2)*(m*r^2)`