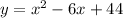Question

The vertex form of the equation of a parabola is y=(x-3)^2+35 what is the standard form of the equation

Answer 1

`y=x^2 -6x+44`

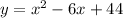
Explanation:

The standard form of a quadratic equation is:

`y = ax ^ 2 + bx + c`.

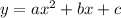In this case we have the following quadratic equation in vertex form

`y=(x-3)^2+35`

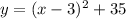
Now we must rewrite the equation in the standard form.

`y=(x-3)(x-3)+35`

Apply the distributive property

`y=x^2 -3x -3x +9+35`

`y=x^2 -6x+9+35`

`y=x^2 -6x+44`

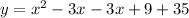
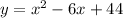
the standard form of the equation is:
`y=x^2 -6x+44`

Answer 2

x^2 -6x+44

Explanation:

Develop form of (x-3)^2 is x^2 - 6x +9

Then y= x^2 -6x +9 + 35

So, y= X^2 -6x +44