Question

The 20-g bullet is travelling at 400 m/s when it becomes embedded in the 2-kg stationary block. The coefficient of kinetic friction between the block and the plane is μk = 0.24. Determine the distance the block will slide before it stops.

Answer 1

The distance the block will slide before it stops is x= 3.4 m .

Step-by-step explanation:

m1= 0,02 kg

V1= 400 m/s

m2= 2 kg

V2= ?

g= 9.8 m/s²

μ= 0.24

N = m2 * g = 19.6 N

Fr= μ * N

Fr= 4.704 N

due to the conservation of the amount of movement:

m1*V1 = m2*V2

V2= 4 m/s

Fr = m2*a

a= Fr/m2

a= -2.352 m/s²

matching momentum and amount of movement

Fr*t=m2*V2

t= 1.7 sec

x= V2*t - (a*t²)/2

x= 3.4 m

Answer 2

The distance the block will slide before it stops is 3.3343 m

Step-by-step explanation:

Given;

mass of bullet, m₁ = 20-g = 0.02 kg

speed of the bullet, u₁ = 400 m/s

mass of block, m₂ = 2-kg

coefficient of kinetic friction, μk = 0.24

Step 1:

Determine the speed of the bullet-block system:

From the principle of conservation of linear momentum;

m₁u₁ + m₂u₂ = v(m₁ + m₂)

where;

v is the speed of the bullet-block system after collision

(0.02 x 400) + (2 x 0) = v (0.02 + 2)

8 = v (2.02)

v = 8/2.02

v = 3.9604 m/s

Step 2:

Determine the time required for the bullet-block system to stop

Apply the principle of conservation momentum of the system

`v(m_1+m_2) -F_kt = v_f(m_1 +m_2)\\\\v(m_1+m_2) -N \mu_kt = v_f(m_1 +m_2)\\\\v(m_1+m_2) -g(m_1 +m_2) \mu_kt = v_f(m_1 +m_2)\\\\3.9604(2.02)-9.8(2.02)0.24t = v_f(2.02)\\\\8 - 4.751t = 2.02v_f\\\\3.9604 - 2.352t = v_f`

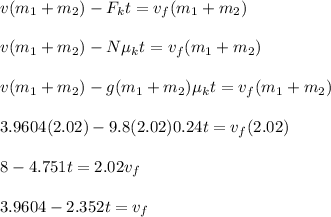
when the system stops, vf = 0

3.9604 -2.352t = 0

2.352t = 3.9604

t = 3.9604/2.352

t = 1.684 s

Thus, time required for the system to stop is 1.684 s

Finally, determine the distance the block will slide before it stops

From kinematic, distance is the product of speed and time

`S = \int\limits {v} \, dt \\\\S = \int\limits^t_0 {(3.9604-2.352t)} \, dt\\\\ S = 3.9604t - 1.176t^2`

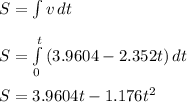
Now, recall that t = 1.684 s

S = 3.9604(1.684) - 1.176(1.684)²

S = 6.6693 - 3.3350

S = 3.3343 m

Thus, the distance the block will slide before it stops is 3.3343 m