Answer:
x = 1/2
Explanation:
The equation in correct format is:
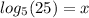
We have to solve this logarithmic equation to find the value of x. This can be done by using the rules of logarithm i.e the power rule and same base rule shown below:
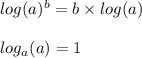
Using these rules on our equation, we get:
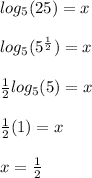
Thus the value of x would be 1/2