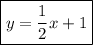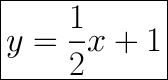
First, we must find the slope of the graphed line. We can use the formula
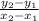 , where
, where
 and
and
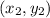 are known points on the line.
are known points on the line.
Plug in the values.
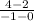
Subtract.
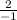
Simplify.
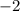
To find the slope of the perpendicular line, we must find the opposite inverse slope. This means we first need to multiply it by
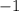 , then we need to swap the numerator and denominator.
, then we need to swap the numerator and denominator.

Now, swap the numerator and denominator. The numerator is
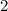 , and the denominator is
, and the denominator is
 by default.
by default.

The only answer choice with a slope of
 is
is