Question

Consider a circle whose equation is x + y - 2x - 8=0. Which statements are true? Select three options

The radius of the circle is 3 units
The center of the circle hes on the x-axis
The center of the orde hes on the y-axis
The standard form of the equation is (x-1)' + y = 3
The radius of this circle is the same as the radius of the circle whose equation is x + y = 9​

Answer 1

The standard form of the equation is

`{(x - 1)}^(2) + {(y - 0)}^(2) = {3}^(2)`

Explanation:

The given circle has equation:

`{x}^(2) + {y}^(2) - 2x - 8 = 0`

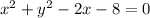
We regroup similar terms to obtain:

`{x}^(2) -2x + {y}^(2) = 8`

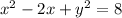
We now complete the square to obtain:

`{x}^(2) -2x + {( - 1)}^(2) + {y}^(2) = 8 + {( - 1)}^(2)`

`{(x - 1)}^(2) + {(y - 0)}^(2) = 9`

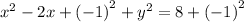
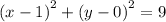
Or

`{(x - 1)}^(2) + {(y - 0)}^(2) = {3}^(2)`

This is now of the form:

`{(x - h)}^(2) + {(y - k)}^(2) = {r}^(2)`

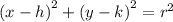
which is referred to as the standard form equation of the circle: