Question

`- 3 + 5i / - 3 - 4i`
​

Answer 1

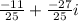`(-11)/(25)+(-27)/(25)i` given you are asked to simplify

`(-3+5i)/(-3-4i)`

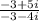
Explanation:

You have to multiply the numerator and denominator by the denominator's conjugate.

The conjugate of a+bi is a-bi.

When you multiply conjugates, you just have to multiply first and last.

(a+bi)(a-bi)

a^2-abi+abi-b^2i^2

a^2+0 -b^2(-1)

a^2+-b^2(-1)

a^2+b^2

See no need to use the whole foil method; the middle terms cancel.

So we are multiplying top and bottom of your fraction by (-3+4i):

`(-3+5i)/(-3-4i) \cdot (-3+4i)/(-3+4i)=((-3+5i)(-3-4i))/((-3-4i)(-3+4i))`

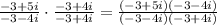
So you will have to use the complete foil method for the numerator. Let's do that:

(-3+5i)(-3+4i)

First: (-3)(-3)=9

Outer:: (-3)(4i)=-12i

Inner: (5i)(-3)=-15i

Last: (5i)(4i)=20i^2=20(-1)=-20

--------------------------------------------Combine like terms:

9-20-12i-15i

Simplify:

-11-27i

Now the bottom (-3-4i)(-3+4i):

F(OI)L (we are skipping OI)

First:-3(-3)=9

Last: -4i(4i)=-16i^2=-16(-1)=16

---------------------------------------------Combine like terms:

9+16=25

So our answer is
`(-11-27i)/(25){/tex] unless you want to seprate the fraction too:</p><p>[tex](-11)/(25)+(-27)/(25)i`