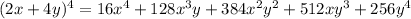(2x + 4y)^4 Expanded using Pascal's triangle or binomial theorem ​

Question

`(2x + 4y)^4`
Expanded using Pascal's triangle or binomial theorem ​

Answer 1

You build Pascal's triangle as follows: every row starts and ends with 1, and every term is the sum of the two immediately above. So, we have

`\begin{array}{c}n=0\\n=1\\n=2\\n=3\\n=4\end{array}\qquad\begin{array}{ccccccccc}&&&&1&&&&\\&&&1&&1&&&\\&&1&&2&&1&&\\&1&&3&&3&&1&\\1&&4&&6&&4&&1\end{array}`

We can use this triangle to expand powers as follows: the binomial
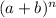`(a+b)^n` will feature all the powers
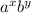`a^xb^y`, where
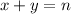`x+y=n`, with some coefficients: in this case, we have

`(a+b)^4 = c_4a^4b^0 + c_3a^3b^1+c_2a^2b^2+c_1a^1b^3+c_0a^0b^4`

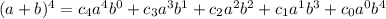
and the coefficients
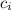`c_i` are exactly the required row of the Pascal's triangle. Removing also unnecessary exponents, we have

`(a+b)^4 = a^4 + 4a^3b+6a^2b^2+4ab^3+b^4`

Finally, substitute a=2x and b=4y to get the answer:

`(2x+4y)^4 = 16 x^4 + 128 x^3 y + 384 x^2 y^2 + 512 x y^3 + 256 y^4`