Question

I need help pretty please!

Answer 1

cos(z) = .3846153846 and angle z = 67.38°

Explanation:

Side UV is corresponding to side YX. Side VW is corresponding to side YZ. Side UW is corresponding to side XZ.

Starting with the first corresponding pair, we are told that side UV is 36, and that side YX is 3/5 of that. So side YX is

`(3)/(5)*36=21.6`

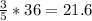
We are next told that side VW is 39, so side YZ is

`(3)/(5)*39=23.4`

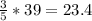
In order to find the cos of angle z, we need the adjacent side, which is side XZ. Side XZ is 3/5 of side UW. Right now we don't know the length of side UW, so we find it using Pythagorean's Theorem:

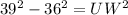`39^2-36^2=UW^2` and

`UW^2=225` so

UW = 15

Now we can say that side XZ is

`(3)/(5)*15=9`

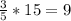
The cos of an angle is the side adjacent to the angle (9) over the hypotenuse of the triangle (23.4) so our ratio is:

`cos(z)=(9)/(23.4)`

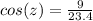
which divides to

cos(z) = .3846153846

If you need the value of the angle, use the inverse cosine function on your calculator in degree mode to find that

angle z = 67.38°