In the xy-plane, a parabola defined by the equation y=(x-8)^2 intersects the line defined by the equation y=36 at two points, P and Q. What is the length of PQ? A) 8 B) 10 C) 12…

Question

asked Mar 16, 2020 1.3k views

1 Answer

Bryan Huang · Answer 1 · 2020-03-22T20:47:27+0000

Answer:

12

Explanation:

Alright so we are asked to find the intersection of y=(x-8)^2 and y=36.

So plug second equation into first giving: 36=(x-8)^2.

36=(x-8)^2

Take square root of both sides:

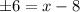
$\pm 6=x-8$

Add 8 on both sides:

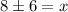
$8 \pm 6=x$

x=8+6=14 or x=8-6=2

So we have the two intersections (14,36) and (2,36).

We are asked to compute this length.

The distance formula is:

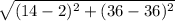
√((14-2)^2+(36-36)^2)

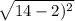
$\sqrt{14-2)^2+(0)^2$

$\sqrt{14-2)^2$

√(12^2)

.

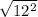
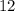I could have just found the distance from 14 and 2 because the y-coordinates were the same. Oh well. 14-2=12.