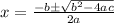Question

Someone please be awesome and help me please :(

Answer 1

`(x+(b)/(2a))^2+((4ac)/(4a^2)-(b^2)/(4a^2))=0`

`(x+(b)/(2a))^2=(b^2-4ac)/(4a^2)`

`x=(-b)/(2a) \pm (√(b^2-4ac))/(2a)`

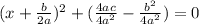
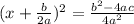
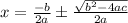
Explanation:

`x^2+(b)/(a)x+(c)/(a)=0`

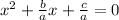
They wanted to complete the square so they took the thing in front of x and divided by 2 then squared. Whatever you add in, you must take out.

`x^2+(b)/(a)x+((b)/(2a))^2+(c)/(a)-((b)/(2a))^2=0`

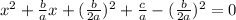
Now we are read to write that one part (the first three terms together) as a square:

`(x+(b)/(2a))^2+(c)/(a)-((b)/(2a))^2=0`

I don't see this but what happens if we find a common denominator for those 2 terms after the square. (b/2a)^2=b^2/4a^2 so we need to multiply that one fraction by 4a/4a.

`(x+(b)/(2a))^2+(4ac)/(4a^2)-(b^2)/(4a^2)=0`

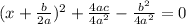
They put it in ( )

`(x+(b)/(2a))^2+((4ac)/(4a^2)-(b^2)/(4a^2))=0`

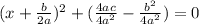
I'm going to go ahead and combine those fractions now:

`(x+(b)/(2a))^2+((-b^2+4ac)/(4a^2))=0`

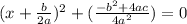
I'm going to factor out a -1 in the second term ( the one in the second ( ) ):

`(x+(b)/(2a))^2-((b^2-4ac)/(4a^2))=0`

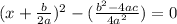
Now I'm going to add (b^2-4ac)/(4a^2) on both sides:

`(x+(b)/(2a))^2=(b^2-4ac)/(4a^2)`

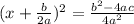
I'm going to square root both sides to rid of the square on the x+b/(2a) part:

`x+(b)/(2a)=\pm \sqrt{(b^2-4ac)/(4a^2)}`

`x+(b)/(2a)=\pm (√(b^2-4ac))/(2a)`

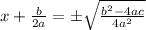
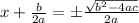
Now subtract b/(2a) on both sides:

`x=(-b)/(2a) \pm (√(b^2-4ac))/(2a)`

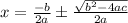
Combine the fractions (they have the same denominator):

`x=(-b \pm √(b^2-4ac))/(2a)`