Question

Identify the radius and center.

x^2 + y^2 - 2x + 4y - 11 = 0

Answer 1

Hello!

The answer is:

Center: (1,-2)

Radius: 4 units.

Why?

To solve the problem, using the given formula of a circle, we need to find its standard equation form which is equal to:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

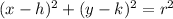
Where,

"h" and "k"are the coordinates of the center of the circle and "r" is its radius.

So, we need to complete the square for both variable "x" and "y".

The given equation is:

`x^2+y^2-2x+4y-11=0`

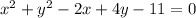
So, solving we have:

`x^2+y^2-2x+4y=11`

`(x^2-2x+((2)/(2))^(2) )+(y^2+4y+((4)/(2))^(2))=11+((2)/(2))^(2) +((4)/(2))^(2)\\\\(x^2-2x+1)+(y^2+4y+4)=11+1+4\\\\(x^2-1)+(y^2+2)=16`

`(x^2-1)+(y^2-(-2))=16`

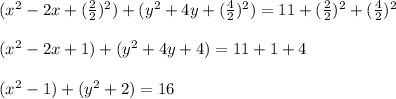
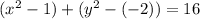
Now, we have that:

`h=1\\k=-2\\r=√(16)=4`

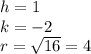
So,

Center: (1,-2)

Radius: 4 units.

Have a nice day!

Note: I have attached a picture for better understanding.