Hello!
The answer is:
The equation of the line that passes through the points (-2,1) and (6,-5) is:
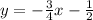
Why?
To solve the problem, we can use the following formula:
We have that:
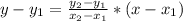
So, using the given points (-2,1) and (6,-5), we have:
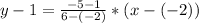
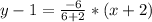
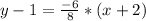
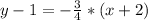
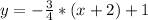
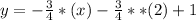
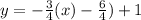
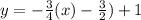
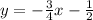
Hence, we have that the equation of the line that passes through the points (-2,1) and (6,-5) is:
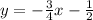
Have a nice day!