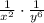Answer:

Explanation:
We are given

First rule I'm going to use is
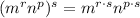 .
.
This gives us:
 is
is
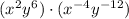 .
.
Now pair up the bases that are the same:
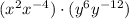 .
.
Add the exponents when multiplying if the bases are the same:
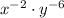
Now usually teachers don't like negative exponents.
To get rid of the negative exponents just take the reciprocal: