Question

Determine whether the relation represents y as a function of x.

1.) x^2+y^2=9


2.) 2xy=1

Answer 1

1 is not a function

2 is a function because you can write it (AS) f(x)=1/(2x).

Explanation:

1) x^2+y^2=9 is a circle with center (0,0) and radius 3.

To get this all I did was compare to (x-h)^2+(y-k)^2=r^2 where (h,k) is the center and r is the radius.

A circle is not a function.

You can solve solve for and see that you will get two values for y which is no go for a function.

Let's do that:

`x^2+y^2=9`

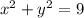
Subtract x^2 on both sides:

`y^2=9-x^2`

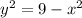
Square root both sides:

`y=\pm √(9-x^2)`.

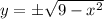2) 2xy=1

Divide both sides by 2x:

y=1/(2x).

This is a function only one y there.