Hello!
The answer is:
The perimeter of the rectangle is equal to 39.32".
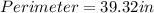
Why?
Since we are working with a rectangle, we can use the Pythagorean theorem to find the missing side of the rectangle and calculate its perimeter. We must remember that we can divide a rectangle into two equal right triangles.
According to the Pythagorean Theorem, we have:

Where:
a, represents the hypotenuse of the triangle which is equal to the diagonal of the given rectangle (14")
b and c are the other sides of the triangle.
Now, let be "a" 14" and "b" 11"
So, solving we have:

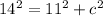
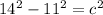
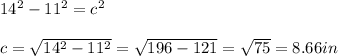
Now, that we already know the the missing side of the rectangle, we can calculate the perimeter using the following formula:
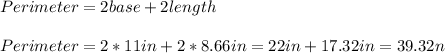
Hence, we have that the perimeter of the rectangle is equal to 39.32".
Have a nice day!