Answer:
Summation notation is:
![\sum_(n=1)^(16)[5(x-1)-9]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ww8pli6uibmrzm0uh1xeh62dszb3ojr4rh.png)
If you prefer it a little more simplified:
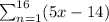
Explanation:
First my favorite part, finding a pattern between the consecutive terms.
This is an arithmetic series because the terms are going up by 5 each time.
So arithmetic sequence, think linear equations:
x | y
1 -9
2 -4
3 1
4 6
..................
n 66
We are going to have to find that n but will will eventually...
The equation for a line in point slope form is
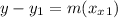 where
where
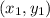 is a point on the line and m is the slope.
is a point on the line and m is the slope.
We are already have the slope is 5 (the slope is the common difference in arithmetic sequence).
I'm going to use the first point (1,-9).
So the equation in point slope form is
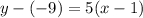
Subtract 9 on both sides:
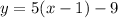
Now we need to know how many terms we are adding so what is x if y=66.
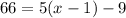
Add 9 on both sides:
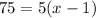
Divide both sides by 5:
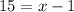
Add 1 on both sides:
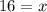
We have 16 terms in this sequence where the 16th term is 66.
Summation notation is:
![\sum_(n=1)^(16)[5(x-1)-9]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ww8pli6uibmrzm0uh1xeh62dszb3ojr4rh.png)
You could simplify the 5(x-1)-9.
Distribute: 5x-5-9
Add like terms: 5x-14