Answer:
Find the explicit from for the sequence
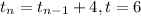 :
:
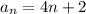
This next question I edited a bit. Your question just says find the four terms. I'm assuming they meant the first four. I also changed the c to an
 .
.
Find the first four terms of the sequence given by:
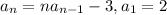 :
:
a) 2,1,0.-3
You might want to read that second question again because there is errors in the question or things that don't really make sense. I made my own interpretation of the problem based on my own mathematical experience.
Explanation:
So your first question actually says that you can find a term by taking that term's previous term and adding 4.
So more terms of the sequence starting at first term 6 is:
6,10,14,18,....
This is an arithmetic sequence. When thinking of arithmetic sequences you should just really by thinking about equations of lines.
Let's say we have this table for (x,y):
x | y
----------
1 6
2 10
3 14
4 18
So we already know the slope which is the common difference of an arithmetic sequence.
We also know point slope form of a line is
 where m is the slope and
where m is the slope and
 is a point on the line. You can use any point on the line. I'm going to use the first point (1,6) with my slope=4.
is a point on the line. You can use any point on the line. I'm going to use the first point (1,6) with my slope=4.
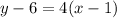
 :I added 6 on both sides here.
:I added 6 on both sides here.
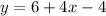 :I distribute here.
:I distribute here.
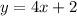 :This is what I get after combining like terms.
:This is what I get after combining like terms.
So
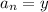 and
and
 so you have:
so you have:
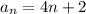
---------------------------------------------------------------------------------------
The first four terms of this sequence will be given by:
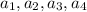
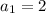 so it is between choice a, c, and d.
so it is between choice a, c, and d.

To find
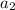 replace n with 2:
replace n with 2:

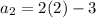
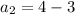
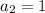
So we have to go another further the only one that has first two terms 2,1 is choice a.