Step-by-step explanation:
The given data is as follows.
J = 3.5 kg-m/s, m = 120 g = 0.120 kg (as 1 g = 0.001 kg)
It is known that formula to calculate impulse is as follows.
J =
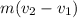
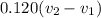 = 3.5
= 3.5
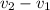 = 29 m/s
= 29 m/s
So,
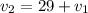
= 29 + 0 = 29 m/s
Thus, we can conclude that final speed (
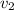 ) is 29 m/s.
) is 29 m/s.