Question

PLEASE HELP

Identify the radius and center


x^2 +y^2 -6x -2y + 1 = 0

Answer 1

The center is the point (3,1) and the radius is 3 units

Explanation:

we know that

The equation of a circle in standard form is equal to

`(x-h)^(2)+(y-k)^(2)=r^(2)`

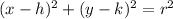
we have

`x^(2)+y^(2)-6x-2y+1=0`

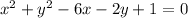
Convert to standard form

Group terms that contain the same variable, and move the constant to the opposite side of the equation

`(x^(2)-6x)+(y^(2)-2y)=-1`

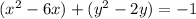
Complete the square twice. Remember to balance the equation by adding the same constants to each side.

`(x^(2)-6x+9)+(y^(2)-2y+1)=-1+9+1`

`(x^(2)-6x+9)+(y^(2)-2y+1)=9`

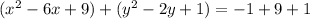
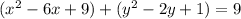
Rewrite as perfect squares

`(x-3)^(2)+(y-1)^(2)=9`

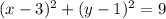
The center is the point (3,1) and the radius is 3 units