Question

PLEASE HELP ASAP! I don’t recall how to do this!

Answer 1

Explanation:

For a. we start by dividing both sides by 200:

`(1.05)^x=1.885`

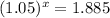
In order to solve for x, we have to get it out from its position of an exponent. Do that by taking the natural log of both sides:

`ln(1.05)^x=ln(1.885)`

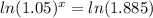
Applying the power rule for logs lets us now bring down the x in front of the ln:

x * ln(1.05) = ln(1.885)

Now we can divide both sides by ln(1.05) to solve for x:

`x=(ln(1.885))/(ln(1.05))`

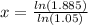
Do this on your calculator to find that

x = 12.99294297

For b. we will first apply the rule for "undoing" the addition of logs by multipllying:

`ln(x*x^2)=5`

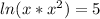
Simplifying gives you

`ln(x^3)=5`

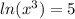
Applying the power rule allows us to bring down the 3 in front of the ln:

3 * ln(x) = 5

Now we can divide both sides by 3 to get

`ln(x)=(5)/(3)`

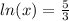
Take the inverse ln by raising each side to e:

`e^(ln(x))=e^{(5)/(3)}`

The "e" and the ln on the left undo each other, leaving you with just x; and raising e to the power or 5/3 gives you that

x = 5.29449005

For c. begin by dividing both sides by 20 to get:

`(1)/(2)=e^(.1x)`

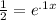
"Undo" that e by taking the ln of both sides:

`ln(.5)=ln(e^(.1x))`

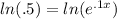
When the ln and the e undo each other on the right you're left with just .1x; on the left we have, from our calculators:

-.6931471806 = .1x

x = -6.931471806

Question d. is a bit more complicated than the others. Begin by turning the base of 4 into a base of 2 so they are "like" in a sense:

`(2^2)^x-6(2)^x=-8`

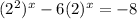
Now we will bring over the -8 by adding:

`(2^2)^x-6(2)^x+8=0`

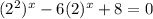
We can turn this into a quadratic of sorts and factor it, but we have to use a u substitution. Let's let
`u=2^x`

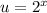
When we do that, we can rewrite the polynomial as

`u^2-6u+8=0`

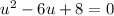
This factors very nicely into u = 4 and u = 2

But don't forget the substitution that we made earlier to make this easy to factor. Now we have to put it back in:

`2^x=4,2^x=2`

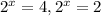
For the first solution, we will change the base of 4 into a 2 again like we did in the beginning:

`2^2=2^x`

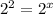
Now that the bases are the same, we can say that

x = 2

For the second solution, we will raise the 2 on the right to a power of 1 to get:

`2^x=2^1`

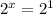
Now that the bases are the same, we can say that

x = 1