Answer:

Explanation:
Given expression

Given information
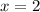
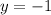

Substitute values into the given expression
![2[2(2)^2+(2)(-1)-(-2)^2]-(2)(-1)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/wk1dh7dhun92g4ngsphe.png)
Simplify the exponents
![2[2(4)+(2)(-1)-(4)]-(2)(-1)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/lao9kyocclnui356zvve.png)
Simplify by multiplication
![2[8-2-4]+2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/fvroylslavon3oxbwcx1.png)
Simplify values in the parenthesis
![2[6-4]+2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/b5k82tlcu2efz8dbaepb.png)
![2[2]+2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/2l78g7o9yeci0abirauj.png)
Simplify by multiplication
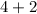

Hope this helps!! :)
Please let me know if you have any questions