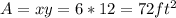Question

Four hundred eighty dollars are available to fence in a rectangular garden. The fencing for the north and south sides of the garden costs $10 per foot and the fencing for the east and west sides costs $20 per foot. Find the dimensions of the largest possible garden.

Answer 1

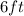`6ft` length on the east and west sides

`12ft` length on the north and south sides

Explanation:

Using x for the length of the east side (and is equal to the length of the west side) and y for the length of the north side (and is equal to the length of the south side), the equation that gives the total price equalized to 480 is:

`20x+20x+10y+10y=480`

`40x+20y=480`

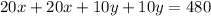
Solving for y

`y=(-40x+480)/(20)`

`y=-2x+24`

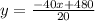
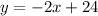
The area of the garden is
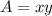`A=xy`, to find the largest, substitute y in the formula of the area

`A=x(-2x+24)=-2x^2+24x`

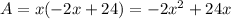
For the optimization, find the largest area, is needed the critical point. To find this point, derive A and equalize the derivative to zero:

`A'=-4x+24=0`

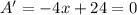
Solve for x:

`-4x=-24`

`x=(-24)/(-4)`

`x=6`

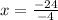
To see if x=6 is a maximum or a minimum, derive A' and substitute with x=6

`A''=-4`

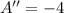
In this case, the second derivative of A doesn't depend on x, and it has a negative value, meaning the value found is a maximum. Using x=6 to find y

`y=-2x+24`

`y=-2(6)+24`

`y=12`

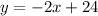
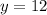
The area is:

`A=xy=6*12=72 ft^2`