Question

Find the area of the triangle with vertices (1, 0, 0), (0, 2, 0), and (0, 0, 1). (Hint: A triangle is half of a parallelogram. Sketching a generic picture may help you visualize before you start to compute.)

Answer 1

1.5 square units.

Explanation:

In order to find the area we can construct a triangle by calculating the sides length using the distance equation:

`distance = \sqrt{(x2-x1)^(2) +(y2-y1)^(2) +(z2-z1)^(2)}`

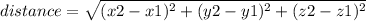
between points (1,0,0) and (0,2,0) the distance is:

`distance = \sqrt{(0-1)^(2) +(2-0)^(2) +(0-0)^(2)}`

`distance = \sqrt{(-1)^(2) +2^(2)}`

`distance = √(5)`

`distance = 2.2361`

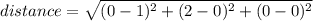
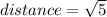
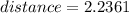
between points (1,0,0) and (0,0,1) the distance is:

`distance = \sqrt{(0-1)^(2) +(0-0)^(2) +(1-0)^(2)}`

`distance = \sqrt{(-1)^(2) +1^(2)}`

`distance = √(2)`

`distance = 1.4142`

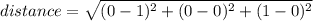
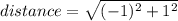
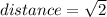
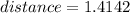
between points (0,2,0) and (0,0,1) the distance is:

`distance = \sqrt{(0-0)^(2) +(0-2)^(2) +(1-0)^(2)}`

`distance = \sqrt{(-2)^(2) +1^(2)}`

`distance = √(5)`

`distance = 2.2361`

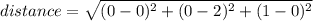
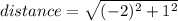
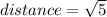
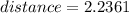
Because we have an isosceles triangle (two sides with equal length) then we can use the following formula for the area:

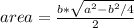`area=\frac{b*\sqrt{a^(2)-b^(2)/4}}{2}` where 'b' is the unique side with different lenght, so:

`area=\frac{1.4142*\sqrt{2.2361^(2)-1.4142^(2)/4}}{2}`

`area=1.5`

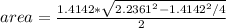
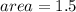
In conclusion the are is 1.5 square units.