Answer:
First option.
Option 5.
Option 6.
Explanation:
The formula for a 30-60-90 triangle is this:
1) Side opposite to 30 will be value
 .
.
2) Side opposite to 60 will be value
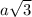 .
.
3) Hypotenuse will be
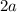 .
.
So let's look and see:
First option:
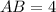 and
and
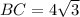
AB is opposite of the angle with 30 degree measurement.
BC is opposite of the angle with 60 degree measurement.
So
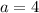 here.
here.
So the side opposite of 60 using the formula should be
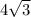 which it is here.
which it is here.
So first option looks good.
Second option:
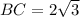 and
and
 .
.
We aren't given the side opposite to 30.
AC is the hypotenuse so 2a=2 which means the side opposite to 30 is a=2/2=1.
This means using the formula that the side opposite to 60 will be
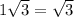 but we don't have that.
but we don't have that.
So not option 2.
Third option:
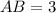 and
and

AB is the side opposite of 30, so we have
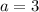
AC is the hypotenuse so that side should be
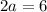 and it isn't.
and it isn't.
Option 3 is not working.
Fourth option:
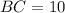 and
and
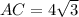
So we have that
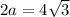 which means
which means
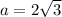 and so
and so
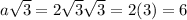 but that is a contradiction because we have this value should be 10.
but that is a contradiction because we have this value should be 10.
Not option 4.
Option 5:
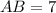 and
and

So we have
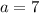 and
and
 so this looks good.
so this looks good.
Option 6:
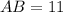 and
and
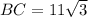
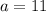 so
so
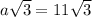 which is what we have.
which is what we have.
Option 6 works.