Answer:
A.
f(x+1)=5/2f(x) with f(1)=3/2
Explanation:
So we are looking for a recursive form of
 .
.
This is the explicit form of a geometric sequence where
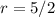 and
and
 .
.
The general form of an explicit equation for a geometric sequence is
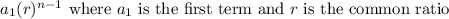 .
.
The recursive form of that sequence is:
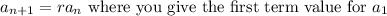 .
.
So we have r=5/2 here so the answer is A.
f(x+1)=5/2f(x) with f(1)=3/2
By the way all this says is term is equal to 5/2 times previous term.