Question

The Kaiser Medical Foundation claims that the cost to rehabilitate a football player following a head injury is at most $28,500. To test this claim a researcher surveys the medical billing records of 45 football players who were treated for head injuries. The average cost for rehabilitation in this randomly selected sample is $30,885 with a standard deviation of $1,123. Is the actual cost of rehabilitation at most $28,500 as Kaiser claims?

Answer 1

Answer: t-statistic > t-critical, we reject the null hypothesis.

Therefore, we conclude that kaiser claim is valid.

Step-by-step explanation:

In this question,

Null hypothesis,
`H_(0)` : Actual cost of rehabilitation is greater than $28,500

Alternative Hypothesis,
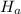`H_(a)` : Actual cost of rehabilitation at most $28,500

the medical billing records of 45 football players, n = 45

\bar{X} ⇒ average cost for rehabilitation = $30,885

`H_(0)`: u > 28500 ⇒ Kaiser claims is not valid

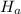`H_(a)`: u ≤ 28500 ⇒ Kaiser claims is valid

t - statistic =
`\frac{\bar{X} - u}{(SD)/(√(n) ) }`

=
`(30885 - 28500)/((1123)/(√(45) ) )`

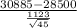
= 14.25

From the t- distribution, with degree of freedom = n-1 ⇒ 45-1 = 44 and level of significance 0.05

t-critical value = 1.6802

So,

t-statistic > t-critical, we reject the null hypothesis.

Therefore, we conclude that kaiser claim is valid.