Question

A manufacturer believes that the cost function

C(x)=5/2x^2+120x+560

approximates the dollar cost of producing x units of a product. The manufacturer believes it cannot make a profit when the marginal cost goes beyond $450. What is the most units the manufacturer can produce and still make a profit? What is the total cost at this level of production?

The manufacturer can make up to________________ units and still make a profit. This leads to a total cost of_________________________ $.

Answer 1

Answer: The manufacturer can make up to 66 units and still make a profit. This leads to a total cost of $19370.

Step-by-step explanation:

Given :

C(x)=
`(5)/(2)x^2+120x+560`

`\because MC = (\delta C(x))/(\delta X)`

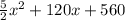
Since the manufacturer believes it cannot make a profit when the marginal cost goes beyond $450.

MC =
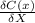`(\delta C(x))/(\delta X)` = $450

On evaluating the above equation , we get ;

x = 66

i.e. At x = 66

C(66) = $19370