Question

Question 11(Multiple Choice Worth 5 points)

(06.03 MC)
What are the solutions for the following system of equations?
-3x² + 4y = 21
4x² + y = 10
O (1,6) and (0, 10)
O (-1, 6) and (1, 6)
O (1, 6) and (3, 12)
O (-1, 6) and (3, 12)

Answer 1

Answer: (-1;6) and (1;6).

Explanation:

`\displaystyle\\\left \{ {{-3x^2+4y=21\ \ \ \ (1)} \atop {4x^2+y=10\ \ \ \ \ (2)}} \right. \\`

Multiply equation (1) by 4, and equation (2) by 3:

`\displaystyle\\\left \{ {{-12x^2+16y=84\ \ \ \ (3)} \atop {12x^2+3y=30\ \ \ \ \ (4)}} \right.\\`

Let us sum up equations (3) and (4):

`19y=114`

Divide both parts of the equation by 19:

`y=6.`

Substitute the value of y into equation (2):

`4x^2+6=10\\4x^2+6-6=10-6\\4x^2=4\\`

Divide both parts of the equation by 4:

`x^2=1\\x^2-1=1-1\\x^2-1=0\\x^2-1^2=0\\`

Let's use the difference-of-squares theorem:

`(x+1)*(x-1)=0\\x+1=0\\x_1=-1.\\x-1=0\\x=1.\\Hence,`

Answer: (-1;6) and (1;6).

Answer 2

(1, 6) and (-1, 6)

Explanation:

Well, we can just solve for y in one of the equations and substitute it into the other equation.

Original equation:

`4x^2+y=10`

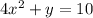
Subtract 4x^2 from both sides

`y=-4x^2+10`

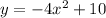
Original Equation:

`-3x^2+4y=21`

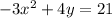
Now substitute in -4x^2+10 as y

`-3x^2+4(-4x^2+10)=21`

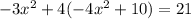
Distribute the 4

`-3x^2-16x^2+40=21`

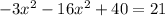
Subtract 21 from both sides and combine like terms

`-19x^2+19`

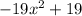
Factor out -19

`-19(x^2-1)`

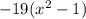
Rewrite using difference of squares

`-19(x-1)(x+1)`

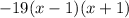
Zeroes at :x=-1 and x=1, since that makes one of the factors zero, thus making the entire thing zero and anything * zero = zero

Now let's just plug in these two values to find the y-values. We can use either equation

`-3(1)^2+4y=21`

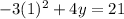
Simplify

`-3+4y=21`

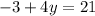
Add 3 to both sides

`4y=24`

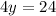
Divide both sides by 4

`y=6`

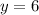
We know that -1, will yield the same thing, since (-1)^2=1, so it's going to have the same y-value of 6.

(1, 6) and (-1, 6)