Answer:
Vertex:
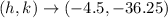
Axis of symmetry:

Explanation:
Finding the Axis of Symmetry:
First I'll find the axis of symmetry. This formula lets us find the a.o.s:
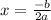 .
.
In
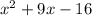 , the values of a, b, and c are:
, the values of a, b, and c are:
We only need a and b to find the axis of symmetry. Substitute these values into the formula.
Simplify this fraction.
The axis of symmetry of this quadratic function is x = -4.5.
Finding the Vertex:
Now to find the vertex, we have to take into account that this quadratic is in standard form, making it a little harder. We have to convert this function into vertex form.
Start by changing f(x) to 'y' and adding 16 to both sides.
Use the completing the square formula:
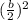
Keep the balance by adding 20.25 on the left side and adding it on the right side of the equation.
Combine like terms.
Factor the right side of the equation. Ask yourself, "What two numbers multiply to 20.25 (c) and add up to 9 (b)?" These two numbers are 4.5 and 4.5. Rewrite the right side with factors.
Isolate y by subtracting 36.25 from both sides of the equation.
Now this quadratic function is in vertex form, making it super simple to find the vertex using
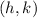 .
.
Vertex form of a quadratic is:
Compare
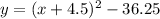 with the original vertex form and find where h and k are. Those are the x (h) and y (k) values of the vertex.
with the original vertex form and find where h and k are. Those are the x (h) and y (k) values of the vertex.
Since the original vertex form has x - h, the h value in
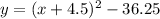 would be a negative since two negatives make a positive. The k value would stay "normal"---negative would mean it is a negative and positive would mean it is a positive number.
would be a negative since two negatives make a positive. The k value would stay "normal"---negative would mean it is a negative and positive would mean it is a positive number.
Therefore the h value is -4.5, and the k value is -36.25.
The ordered pair of the vertex is
 .
.