Question

Use the compound interest formula A =​P(1 + ​r) t and the given information to solve for r.

A =​$2300​, P =​$1600​, t =6 r =?

Answer 1

Rounding to nearest hundredths gives us r=0.06.

So r is about 6%.

Explanation:

So we are given:

`A=P(1+r)^t`

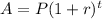
where

`A=2300`

`P=1600`

`t=6`.

`A=P(1+r)^t`

`2300=1600(1+r)^6`

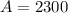
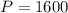
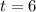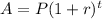
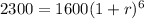
Divide both sides by 1600:

`(2300)/(1600)=(1+r)^6`

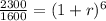
Simplify:

`(23)/(16)=(1+r)^6`

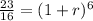
Take the 6th root of both sides:

`\sqrt[6]{(23)/(16)}=1+r`

Subtract 1 on both sides:

`\sqrt[6]{(23)/(16)}-1=r`

So the exact solution is
`r=\sqrt[6]{(23)/(16)}-1`

Most likely we are asked to round to a certain place value.

I'm going to put my value for r into my calculator.

r=0.062350864

Rounding to nearest hundredths gives us r=0.06.