Question

You are choosing 3 of your 7 trophies and arranging them in a row on a shelf.

In how many different ways can you choose and arrange the trophies?

Answer 1

21

Explanation:

you can arrange 7×3 ways

Answer 2

Answer with explanation:

Number of trophies possessed by me= 7

Number of trophies that is to be selected from 7 trophies =3

⇒⇒So, Chosing 3 out of 7 trophies and arranging them on a shelf requires Concept of Permutation, as order of arrangement is also taken into consideration

`=_(3)^(7)\textrm{P}\\\\=(7!)/((7-3)!)\\\\=(7!)/(4!)\\\\=(4!*5*6*7)/(4!)\\\\=5*6*7\\\\=210\text{Ways}`

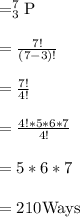
Or

⇒First place can be filled in 7 ways,second place can be filled in 6 ways and third place can be filled in 5 ways.

So total number of ways of selecting 3 trophies from 7 trophies

=7 *6 *5

=210 ways

⇒Now, 3 trophies can be arranged in a shelf in 3! =3 *2*1=6 ways.