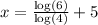Answer:
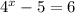 gives the solution
gives the solution
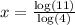 .
.
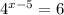 gives the solution
gives the solution
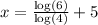 .
.
Explanation:
I will solve both interpretations.
If we assume the equation is
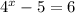 , then the following is the process:
, then the following is the process:
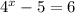
Add 5 on both sides:
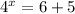
Simplify:
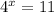
Now write an equivalent logarithm form:
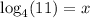
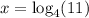
Now using the change of base:
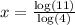 .
.
If we assume the equation is
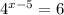 , then we use the following process:
, then we use the following process:
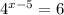
Write an equivalent logarithm form:
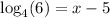
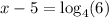
Add 5 on both sides:
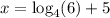
Use change of base formula: