Answer:
The two integers are: 4 and 11.
Explanation:
We are given that one positive integer is 7 less than another. Given that the product of two integers is 44, we are to find the integers.
Assuming
 to be one positive integer and
to be one positive integer and
 to be the other, we can write it as:
to be the other, we can write it as:
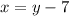 --- (1)
--- (1)
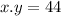 --- (2)
--- (2)
Substituting x from (1) in (2):

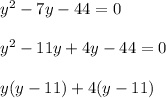
y = 11
Substituting y = 11 in (1) to find x:

x = 4